(本小题满分12分)某学校就一问题进行内部问卷调查.已知该学校有男学生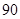 人,女学生
人,女学生 人,教师
人,教师 人,用分层抽样的方法从中抽取
人,用分层抽样的方法从中抽取 人进行问卷调查.问卷调查的问题设置为“同意”、“不同意”两种,且每人都做一种选择.下面表格中提供了被调查人答卷情况的部分信息.
人进行问卷调查.问卷调查的问题设置为“同意”、“不同意”两种,且每人都做一种选择.下面表格中提供了被调查人答卷情况的部分信息.
(1)请完成此统计表;
(2)根据此次调查,估计全校对这一问题持“同意”意见的人数;
(3)从被调查的女学生中选取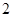 人进行访谈,求选到两名学生中恰有一人“同意”、一人“不同意”的概率.
人进行访谈,求选到两名学生中恰有一人“同意”、一人“不同意”的概率.
推荐套卷
(本小题满分12分)某学校就一问题进行内部问卷调查.已知该学校有男学生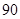 人,女学生
人,女学生 人,教师
人,教师 人,用分层抽样的方法从中抽取
人,用分层抽样的方法从中抽取 人进行问卷调查.问卷调查的问题设置为“同意”、“不同意”两种,且每人都做一种选择.下面表格中提供了被调查人答卷情况的部分信息.
人进行问卷调查.问卷调查的问题设置为“同意”、“不同意”两种,且每人都做一种选择.下面表格中提供了被调查人答卷情况的部分信息.
(1)请完成此统计表;
(2)根据此次调查,估计全校对这一问题持“同意”意见的人数;
(3)从被调查的女学生中选取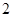 人进行访谈,求选到两名学生中恰有一人“同意”、一人“不同意”的概率.
人进行访谈,求选到两名学生中恰有一人“同意”、一人“不同意”的概率.