（本小题满分为10分）如图，将长为4，宽为1的长方形折叠成长方体ABCD-A1B1C1D1的四个侧面，记底面上一边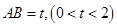
，连接A1B，A1C，A1D．
（1）当长方体ABCD-A1B1C1D1的体积最大时，求二面角B-A1C-D的值；
（2）线段A1C上是否存在一点P，使得A1C
平面BPD，若有，求出P点的位置，没有请说明理由．
的定义域.
－α)＝
，求cos(
π＋α)＋sin2(α－
，求f(α)的值；
相关知识点
推荐套卷
（本小题满分为10分）如图，将长为4，宽为1的长方形折叠成长方体ABCD-A1B1C1D1的四个侧面，记底面上一边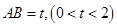，连接A1B，A1C，A1D．
（1）当长方体ABCD-A1B1C1D1的体积最大时，求二面角B-A1C-D的值；
（2）线段A1C上是否存在一点P，使得A1C平面BPD，若有，求出P点的位置，没有请说明理由．
粤公网安备 44130202000953号