(本小题满分13分)如图所示的“8”字形曲线是由两个关于 轴对称的半圆和一个双曲线的一部分组成的图形,其中上半个圆所在圆方程是
轴对称的半圆和一个双曲线的一部分组成的图形,其中上半个圆所在圆方程是 ,双曲线的左、右顶点
,双曲线的左、右顶点 、
、 是该圆与
是该圆与 轴的交点,双曲线与半圆相交于与
轴的交点,双曲线与半圆相交于与 轴平行的直径的两端点.
轴平行的直径的两端点.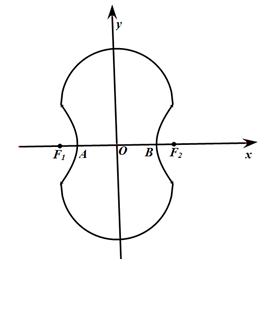
(1)试求双曲线的标准方程;
(2)记双曲线的左、右焦点为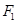 、
、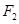 ,试在“8”字形曲线上求点
,试在“8”字形曲线上求点 ,使得
,使得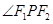 是直角.
是直角.
相关知识点
推荐套卷
(本小题满分13分)如图所示的“8”字形曲线是由两个关于 轴对称的半圆和一个双曲线的一部分组成的图形,其中上半个圆所在圆方程是
轴对称的半圆和一个双曲线的一部分组成的图形,其中上半个圆所在圆方程是 ,双曲线的左、右顶点
,双曲线的左、右顶点 、
、 是该圆与
是该圆与 轴的交点,双曲线与半圆相交于与
轴的交点,双曲线与半圆相交于与 轴平行的直径的两端点.
轴平行的直径的两端点.
(1)试求双曲线的标准方程;
(2)记双曲线的左、右焦点为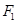 、
、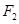 ,试在“8”字形曲线上求点
,试在“8”字形曲线上求点 ,使得
,使得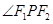 是直角.
是直角.