(本小题满分12分)在如图所示的几何体中,四边形ABCD是等腰梯形,AB//CD,∠ABC=60°,AB=2CB=2.在梯形ACEF中,EF//AC,且 平面ABCD.
平面ABCD.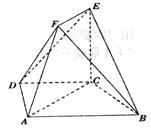
(Ⅰ)求证: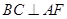 ;
;
(Ⅱ)若二面角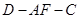 为45°,求CE的长.
为45°,求CE的长.
相关知识点
推荐套卷
(本小题满分12分)在如图所示的几何体中,四边形ABCD是等腰梯形,AB//CD,∠ABC=60°,AB=2CB=2.在梯形ACEF中,EF//AC,且 平面ABCD.
平面ABCD.
(Ⅰ)求证: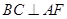 ;
;
(Ⅱ)若二面角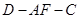 为45°,求CE的长.
为45°,求CE的长.