本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分
(文)对于曲线 ,若存在非负实数
,若存在非负实数 和
和 ,使得曲线
,使得曲线 上任意一点
上任意一点 ,
, 恒成立(其中
恒成立(其中 为坐标原点),则称曲线
为坐标原点),则称曲线 为有界曲线,且称
为有界曲线,且称 的最小值
的最小值 为曲线
为曲线 的外确界,
的外确界, 的最大值
的最大值 为曲线
为曲线 的内确界.
的内确界.
(1)写出曲线 的外确界
的外确界 与内确界
与内确界 ;
;
(2)曲线 与曲线
与曲线 是否为有界曲线?若是,求出其外确界与内确界;若不是,请说明理由;
是否为有界曲线?若是,求出其外确界与内确界;若不是,请说明理由;
(3)已知曲线 上任意一点
上任意一点 到定点
到定点 的距离之积为常数
的距离之积为常数 ,求曲线
,求曲线 的外确界与内确界.
的外确界与内确界.
相关知识点
推荐套卷
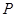 为
为 轴上的动点,点
轴上的动点,点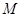 为
为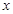 轴上的动点.点
轴上的动点.点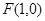 为定点,且满足
为定点,且满足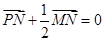 ,
,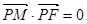
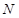 的轨迹
的轨迹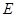 的方程.
的方程.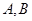 是
是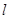 为
为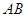 的中垂线,求当
的中垂线,求当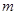 的范围.
的范围. 公里的地铁票价如下表:
公里的地铁票价如下表: (单位:
(单位: )
)





 公里的概率分别为
公里的概率分别为 ,
, ,甲、乙乘车超过
,甲、乙乘车超过 公里的概率分别为
公里的概率分别为 ,
, ,求
,求 中,
中,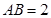 ,
, ,将
,将 沿矩形的对角线
沿矩形的对角线 翻折,得到如图2所示的几何体
翻折,得到如图2所示的几何体 ,使得
,使得 =
= .
.
 ;
; 上存在点
上存在点 ,使得
,使得 ,求二面角
,求二面角 的余弦值.
的余弦值. 的各项均为正数,
的各项均为正数, 为其前
为其前 项和,对于任意
项和,对于任意 ,总有
,总有 成等差数列.
成等差数列. ,数列
,数列 的前
的前 ,求证:
,求证: .
. ,集合
,集合 ,
, 中满足条件“
中满足条件“ ”的元素个数记为
”的元素个数记为 .
. 和
和 的值;
的值; 时,求证:
时,求证: .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号