问题1如图①,一张三角形ABC纸片,点D、E分别是△ABC边上两点.
研究(1):如果沿直线DE折叠,使A点落在CE上,则∠BDA′与∠A的数量关系是什么?
研究(2):如果折成图②的形状,猜想∠BDA′、∠CEA′和∠A的数量关系是什么?
研究(3):如果折成图③的形状,猜想∠BDA′、∠CEA′和∠A的数量关系,并说明理由.
研究(4):将问题1推广,如图④,将四边形ABCD纸片沿EF折叠,使点A、B落在四边形EFCD的内部时,∠1+∠2与∠A、∠B之间的数量关系是什么?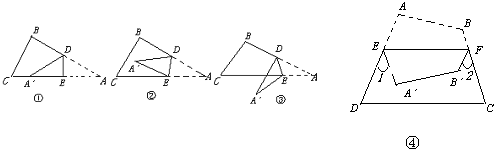
推荐套卷
问题1如图①,一张三角形ABC纸片,点D、E分别是△ABC边上两点.
研究(1):如果沿直线DE折叠,使A点落在CE上,则∠BDA′与∠A的数量关系是什么?
研究(2):如果折成图②的形状,猜想∠BDA′、∠CEA′和∠A的数量关系是什么?
研究(3):如果折成图③的形状,猜想∠BDA′、∠CEA′和∠A的数量关系,并说明理由.
研究(4):将问题1推广,如图④,将四边形ABCD纸片沿EF折叠,使点A、B落在四边形EFCD的内部时,∠1+∠2与∠A、∠B之间的数量关系是什么?