（本小题满分14分）
设△ABC三个内角A、B、C所对的边分别为a，b，c. 已知C＝
，acosA=bcosB．
（1）求角A的大小；
（2）如图，在△ABC的外角∠ACD内取一点P，使得PC＝2．过点P分别作直线CA、CD的垂线PM、PN，垂足分别是M、N．设∠PCA＝α，求PM＋PN的最大值及此时α的取值．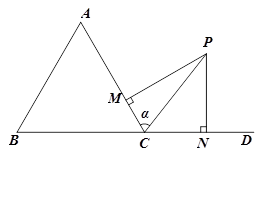
相关试题
，当
时，有
，
的值，使
与
都是有限的．
A∩B,且A∩C=推荐套卷
（本小题满分14分）
设△ABC三个内角A、B、C所对的边分别为a，b，c. 已知C＝，acosA=bcosB．
（1）求角A的大小；
（2）如图，在△ABC的外角∠ACD内取一点P，使得PC＝2．过点P分别作直线CA、CD的垂线PM、PN，垂足分别是M、N．设∠PCA＝α，求PM＋PN的最大值及此时α的取值．
粤公网安备 44130202000953号