（本小题满分12分）
在平面直角坐标系中，有三个点的坐标分别是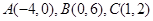
.
（1）证明：A，B，C三点不共线；
（2）求过A，B的中点且与直线
平行的直线方程；
（3）设过C且与AB所在的直线垂直的直线为
，求与两坐标轴围成的三角形的面积.
，画出程序框图．推荐套卷
（本小题满分12分）
在平面直角坐标系中，有三个点的坐标分别是.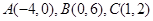
（1）证明：A，B，C三点不共线；
（2）求过A，B的中点且与直线平行的直线方程；
（3）设过C且与AB所在的直线垂直的直线为，求与两坐标轴围成的三角形的面积.
粤公网安备 44130202000953号