（本题10分）已知△ABC为等边三角形，点D为直线BC上一动点（点D不与点B、点C重合）．以AD为边作等边三角形ADE，连接CE．
(1)如图，当点D在边BC上时．①求证：△ABD≌△ACE；②直接判断结论BC=DC+CE是否成立（不需证明）；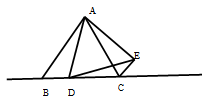
(2)、如图，当点D在边BC的延长线上时，其他条件不变，请写出BC、DC、CE之间存在的数量关系，并写出证明过程.
如图，△ABC中，AB=AC，∠BAC=40°，将△ABC绕点A按逆时针方向旋转100°．得到△ADE，连接BD，CE交于点F．
（1）求证：△ABD≌△ACE；
（2）求∠ACE的度数；
（3）求证：四边形ABFE是菱形．
已知：如图，在平面直角坐标系中，直线AB与反比例函数y=
（m＞0）的图象交与点A（1，4）、B（a、b），q其中a＞1．过点A作x轴的垂线，垂足为C，过点B作y轴的垂线，垂足为D，AC与BD相交于点M，连接CD．
（1）求该反比例函数的解析式；
（2）求证：CD∥AB．
已知代数式
，请解答下列问题：
（1）当x=2sin30°+tan60°时，求原代数式的值；
（2）当x在实数范围内取值时，原代数式的值能等于-1吗？说明理由．
如图1，A1B1和A2B2是水面上相邻的两条赛道（看成两条互相平行的线段）．甲是一名游泳运动健将，乙是一名游泳爱好者，甲在赛道A1B1上从A1处出发，到达B1后，以同样的速度返回A1处，然后重复上述过程；乙在赛道A2B2上以2m/s的速度从B2处出发，到达A2后以相同的速度回到B2处，然后重复上述过程（不考虑每次折返时的减速和转向时间）．若甲、乙两人同时出发，设离开池边B1B2的距离为y（m），运动时间为t（s），甲游动时，y（m）与t（s）的函数图象如图2所示．
（1）赛道的长度是m，甲的速度是m/s；
（2）经过多少秒时，甲、乙两人第二次相遇？
（3）若从甲、乙两人同时开始出发到2分钟为止，甲、乙共相遇了次．2分钟时，乙距池边B1B2的距离为多少米．
，求⊙O的半径和线段PB的长；
粤公网安备 44130202000953号