选修4-1:几何证明选讲(本小题满分10分)
如下图,AB、CD是圆的两条平行弦,BE//AC,BE交CD于E、交圆于F,过A点的切线交DC的延长线于P,PC=ED=1,PA=2.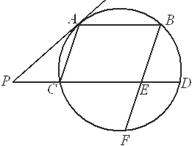
(1)求AC的长;
(2)求证:BE = EF.
推荐套卷
选修4-1:几何证明选讲(本小题满分10分)
如下图,AB、CD是圆的两条平行弦,BE//AC,BE交CD于E、交圆于F,过A点的切线交DC的延长线于P,PC=ED=1,PA=2.
(1)求AC的长;
(2)求证:BE = EF.