在一个不透明的袋子中装有(除颜色外)完全相同的红色小球1个,白色小球1个和黄色小球2个,
(1)从中先摸出一个小球,记录下它的颜色后,将它放回袋中搅匀,再摸出一个小球,记录下颜色. 求摸出的两个小球的颜色恰好是“一红一黄”的概率是多少?
(2)如果摸出第一个小球之后不放回袋中,再摸出第二个小球,这时摸出的两个小球的颜色恰好是“一红一黄”的概率是多少?
(3)小明想给袋中加入一些红色的小球,使从袋中任意摸出一个小球恰为红色的概率为 ,请你帮小明算一算,应该加入多少个红色的小球?
,请你帮小明算一算,应该加入多少个红色的小球?
相关知识点
推荐套卷
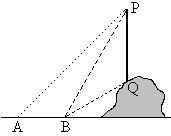
 0.57,cos35°
0.57,cos35°
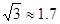 ,
,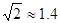


 粤公网安备 44130202000953号
粤公网安备 44130202000953号