用正方形硬纸板做三棱柱盒子，每个盒子由3个矩形侧面和2个正三角形底面组成，硬纸板以如图两种方法裁剪（裁剪后边角料不再利用）
A方法：剪6个侧面； B方法：剪4个侧面和5个底面。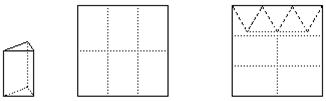
A方法 B方法
现有38张硬纸板，裁剪时x张用A方法，其余用B方法。
(1)、用x的代数式分别表示裁剪出的侧面和底面的个数；
(2)、若裁剪出的侧面和底面恰好全部用完，问能做多少个盒子？
相关试题
（本题 8 分，每小题4分）作图：如图，平面内有A，B，C，D四点 按下列语句画图：
（1）画射线AB，直线BC，线段AC;
（2）连接AD与BC相交于点E.
，其中a = －3.
：
粤公网安备 44130202000953号