某校校园超市老板到批发中心选购甲、乙两种品牌的文具盒,乙品牌的进货单价是甲品牌进货单价的2倍,考虑各种因素,预计购进乙品牌文具盒的数量y(个)与甲品牌文具盒的数量x(个)之间的函数关系如图所示.当购进的甲、乙品牌的文具盒中,甲有120个时,购进甲、乙品牌文具盒共需7200元.
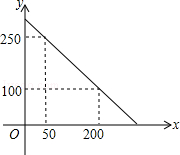
(1)根据图象,求y与x之间的函数关系式;
(2)求甲、乙两种品牌的文具盒进货单价;
(3)若该超市每销售1个甲种品牌的文具盒可获利4元,每销售1个乙种品牌的文具盒可获利9元,根据学生需求,超市老板决定,准备用不超过6300元购进甲、乙两种品牌的文具盒,且这两种品牌的文具盒全部售出后获利不低于1795元,问该超市有几种进货方案?哪种方案能使获利最大?最大获利为多少元?