已知抛物线y1=ax2+bx+c(a≠0)的顶点坐标是(1,4),它与直线y2=x+1的一个交点的横坐标为2.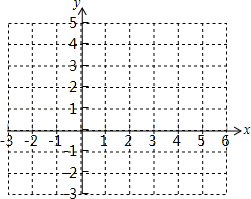
(1)求抛物线的解析式;
(2)在给出的坐标系中画出抛物线y1=ax2+bx+c(a≠0)及直线y2=x+1的图象,并根据图象,直接写出使得y1≥y2的x的取值范围;
(3)设抛物线与x轴的右边交点为A,过点A作x轴的垂线,交直线y2=x+1于点B,点P在抛物线上,当S△PAB≤6时,求点P的横坐标x的取值范围.
相关知识点
推荐套卷
已知抛物线y1=ax2+bx+c(a≠0)的顶点坐标是(1,4),它与直线y2=x+1的一个交点的横坐标为2.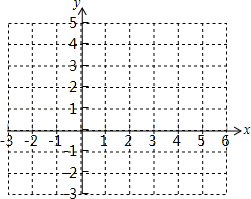
(1)求抛物线的解析式;
(2)在给出的坐标系中画出抛物线y1=ax2+bx+c(a≠0)及直线y2=x+1的图象,并根据图象,直接写出使得y1≥y2的x的取值范围;
(3)设抛物线与x轴的右边交点为A,过点A作x轴的垂线,交直线y2=x+1于点B,点P在抛物线上,当S△PAB≤6时,求点P的横坐标x的取值范围.