（1）.如图①，已知AB∥CD，求证：∠A+∠C=∠E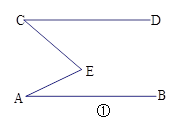
（2）直接写出当点E的位置分别如图②、图③、图④的情形时∠A、∠C、∠E之间的关系.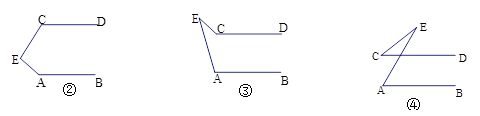
②中∠C、∠A、∠AEC之间的关系为 ；
③中∠C、∠A、∠AEC之间的关系为 ；
④中∠C、∠A、∠AEC之间的关系为 ；
（3）在（2）中的3中情形中任选一种进行证明.
相关试题
如图，已知点A、B、C的坐标分别为（0，0），（4，0），（5， 2）将△ABC绕点A按逆时针方向旋转90°得到△AB′C′．
（1）画出△AB′C′；
（2）求点C′的坐标．
（m为常数）经过点A（2，-1），求反比例函数的解析式．
，其中
（m）是球的飞行高度，
（m）是球飞出的水平距离，结果球离球洞的水平距离还有2m．
粤公网安备 44130202000953号