如图是一个半圆形湖面景点的平面示意图.已知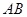 为直径,且
为直径,且 km,
km,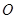 为圆心,
为圆心, 为圆周上靠近
为圆周上靠近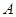 的一点,
的一点,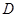 为圆周上靠近
为圆周上靠近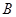 的一点,且
的一点,且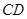 ∥
∥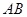 .现在准备从
.现在准备从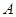 经过
经过 到
到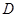 建造一条观光路线,其中
建造一条观光路线,其中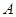 到
到 是圆弧
是圆弧 ,
, 到
到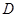 是线段
是线段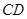 .设
.设 ,观光路线总长为
,观光路线总长为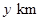 .
.
(1)求 关于
关于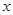 的函数解析式,并指出该函数的定义域;
的函数解析式,并指出该函数的定义域;
(2)求观光路线总长的最大值.
推荐套卷
如图是一个半圆形湖面景点的平面示意图.已知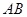 为直径,且
为直径,且 km,
km,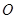 为圆心,
为圆心, 为圆周上靠近
为圆周上靠近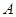 的一点,
的一点,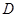 为圆周上靠近
为圆周上靠近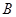 的一点,且
的一点,且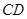 ∥
∥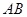 .现在准备从
.现在准备从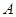 经过
经过 到
到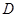 建造一条观光路线,其中
建造一条观光路线,其中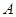 到
到 是圆弧
是圆弧 ,
, 到
到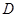 是线段
是线段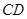 .设
.设 ,观光路线总长为
,观光路线总长为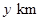 .
.
(1)求 关于
关于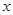 的函数解析式,并指出该函数的定义域;
的函数解析式,并指出该函数的定义域;
(2)求观光路线总长的最大值.