如图,二次函数y=ax2+bx+c的图象的顶点C的坐标为(0,-2),交x轴于A、B两点,其中A(-1,0),直线l:x=m(m>1)与x轴交于D.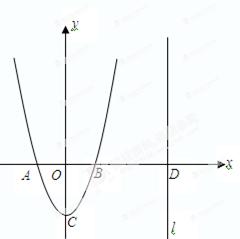
(1)求二次函数的解析式和B的坐标;
(2)在直线l上找点P(P在第一象限),使得以P、D、B为顶点的三角形与以B、C、O为顶点的三角形相似,求点P的坐标(用含m的代数式表示);
(3)在(2)成立的条件下,在抛物线上是否存在第一象限内的点Q,使△BPQ是以P为直角顶点的等腰直角三角形?如果存在,请求出点Q的坐标;如果不存在,请说明理由.
相关知识点
推荐套卷

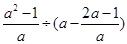 .
. ;当y=4时,x2-1=4,
;当y=4时,x2-1=4, ,
,
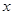 元,每周销量为
元,每周销量为 件。
件。
 粤公网安备 44130202000953号
粤公网安备 44130202000953号