小王玩游戏：一张纸片，第一次将其撕成四小片，以后每次都将其中一片撕成更小的四片，如此进行下去。
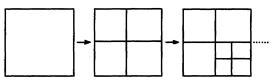
（1）填空：当小王撕了3次后，共有 张纸片；
（2）填空：当小王撕了n次后，共有 张纸片．（用含n的代数式表示）
（3）小王说：我撕了若干次后，共有纸片2013张，小王说的对不对？若不对，请说明你的理由；若对的，请指出小王需撕多少次？
相关试题
已知，如图，四边形ABCD内接于圆，延长AD、BC相交于点E，点F是BD的延长线上的点，且DE平分∠CDF．
（1）求证：AB＝AC；
（2）若AC＝3cm，AD＝2cm，求DE的长．
是圆O的一条弦，
，垂足为
，交圆O于点
，点
在圆O上．
，求
的度数；
，CD=1，求圆O的半径．如图，在平面直角坐标系中，O为原点，每个小方格的边长为1个单位长度．在第一象限内有横、纵坐标均为整数的A、B两点，且OA= OB=
．
（1）写出A、B两点的坐标；
（2）将线段AB绕点O旋转一周，求所形成的图形的面积（结果保留π）．
有两个相等的实数根，求
的值．
粤公网安备 44130202000953号