现有一个长、宽、高分别为5 dm、4 dm、3 dm的无盖长方体木箱(如图,AB=5 dm,BC=4 dm,AE=3 dm).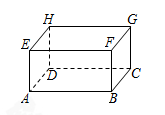
(1)求线段BG的长;
(2)现在箱外的点A处有一只蜘蛛,箱内的点G处有一只小虫正在午睡,保持不动.请你为蜘蛛设计一种捕虫方案,使得蜘蛛能以最短的路程捕捉到小虫.
(请计算说明,木板的厚度忽略不计)
相关知识点
推荐套卷
现有一个长、宽、高分别为5 dm、4 dm、3 dm的无盖长方体木箱(如图,AB=5 dm,BC=4 dm,AE=3 dm).
(1)求线段BG的长;
(2)现在箱外的点A处有一只蜘蛛,箱内的点G处有一只小虫正在午睡,保持不动.请你为蜘蛛设计一种捕虫方案,使得蜘蛛能以最短的路程捕捉到小虫.
(请计算说明,木板的厚度忽略不计)