已知椭圆的焦点坐标是
，
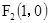，过点
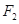垂直于长轴的直线交椭圆与
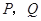两点, 且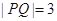
.
（1）求椭圆的方程.
（2）过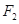的直线与椭圆交于不同的两点
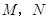, 则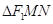
的内切圆面积是否存在最大值?若存在, 则求出这个最大值及此时的直线方程; 若不存在,请说明理由.
和直线l垂直的直线方程；
,在x轴上的截距是-7,求l的方程.
,在x轴上的截距是-7,求l的方程.推荐套卷
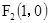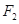已知椭圆的焦点坐标是，，过点垂直于长轴的直线交椭圆与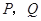两点, 且.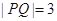
（1）求椭圆的方程.
（2）过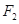的直线与椭圆交于不同的两点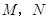, 则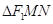的内切圆面积是否存在最大值?若存在, 则求出这个最大值及此时的直线方程; 若不存在,请说明理由.
粤公网安备 44130202000953号