(本小题满分12分)已知焦点在 轴,顶点在原点的抛物线
轴,顶点在原点的抛物线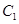 经过点
经过点 ,以抛物线
,以抛物线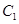 上
上
一点 为圆心的圆过定点
为圆心的圆过定点 (0,1),记
(0,1),记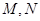 为圆
为圆 与
与 轴的两个交点.
轴的两个交点.
(1)求抛物线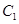 的方程;
的方程;
(2)当圆心 在抛物线上运动时,试判断
在抛物线上运动时,试判断 是否为一定值?请证明你的结论;
是否为一定值?请证明你的结论;
(3)当圆心 在抛物线上运动时,记
在抛物线上运动时,记 ,
, ,求
,求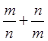 的最大值.
的最大值.
相关知识点
推荐套卷
(本小题满分12分)已知焦点在 轴,顶点在原点的抛物线
轴,顶点在原点的抛物线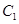 经过点
经过点 ,以抛物线
,以抛物线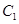 上
上
一点 为圆心的圆过定点
为圆心的圆过定点 (0,1),记
(0,1),记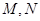 为圆
为圆 与
与 轴的两个交点.
轴的两个交点.
(1)求抛物线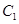 的方程;
的方程;
(2)当圆心 在抛物线上运动时,试判断
在抛物线上运动时,试判断 是否为一定值?请证明你的结论;
是否为一定值?请证明你的结论;
(3)当圆心 在抛物线上运动时,记
在抛物线上运动时,记 ,
, ,求
,求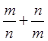 的最大值.
的最大值.