(本小题满分13分)如图,某工厂生产的一种无盖纸筒为圆锥形,现一客户订制该圆锥纸筒,并要求该圆锥纸筒的容积为π立方分米.设圆锥纸筒底面半径为r分米,高为h分米.
(1)求出r与h满足的关系式;
(2)工厂要求制作该纸筒的材料最省,求最省时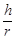 的值.
的值.
推荐套卷
(本小题满分13分)如图,某工厂生产的一种无盖纸筒为圆锥形,现一客户订制该圆锥纸筒,并要求该圆锥纸筒的容积为π立方分米.设圆锥纸筒底面半径为r分米,高为h分米.
(1)求出r与h满足的关系式;
(2)工厂要求制作该纸筒的材料最省,求最省时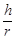 的值.
的值.