为了缓解交通压力，某省在两个城市之间特修一条专用铁路，用一列火车作为公共交通车。已知每日来回趟数
是每次拖挂车厢节数
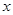的一次函数，如果该列火车每次拖
节车厢，每日能来回
趟；如果每次拖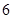
节车厢，则每日能来回
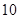趟，火车每日每次拖挂车厢的节数是相同的，每节车厢满载时能载客
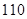人。
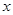（1）求出关于的函数；
（2）该火车满载时每次拖挂多少节车厢才能使每日营运人数最多？并求出每天最多的营运人数？
相关试题
的前
项和为
，且对任意正整数
都在直线
上．求数列
设
求：数列
前
．
是正数组成的数列，其前
项和为
，且对所有的正整数
与2的等差中项等于
的前n项和为Sn，且满足
中，A、B、C的对边分别是a、b、c，且A、B、C成等差数列．
． 
，求:a,c的值．推荐套卷
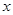为了缓解交通压力，某省在两个城市之间特修一条专用铁路，用一列火车作为公共交通车。已知每日来回趟数是每次拖挂车厢节数的一次函数，如果该列火车每次拖节车厢，每日能来回趟；如果每次拖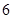节车厢，则每日能来回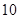趟，火车每日每次拖挂车厢的节数是相同的，每节车厢满载时能载客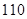人。
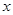（1）求出关于的函数；
（2）该火车满载时每次拖挂多少节车厢才能使每日营运人数最多？并求出每天最多的营运人数？
粤公网安备 44130202000953号