（本小题满分12分）已知向量m＝（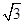
sinωx，cosωx），n＝（cosωx,－cosωx）,若函数f（x）＝m·n的图象关于直线
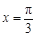对称，其中ω取所有可能值中的最小正数值.
（Ⅰ）求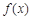
的周期和单调递增区间；
（Ⅱ）△ABC中，如果f（
）＝
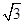，b＝4，且asinA－bsinB＝sinC（c－
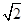b），求△ABC的面积.
相关试题
的离心率
，
是其左右焦点，点
是直线
（其中
）上一点，且直线
的倾斜角为
.
的方程； 
是椭圆
，求
（
为坐标原点）面积的最小值.
（Ⅰ）若函数
在
上单调递减，在区间
单调递增，求
的值；
在
上有两个不同的极值点，求
的取值范围；
有且只有三个不同的实根，求
的前n项和为
，且
．
，数列
的前n项和为
，若不等式
对任意
恒成立，求实数
的取值范围．
，在直角梯形
中，
，
∥
，
，
，将
沿
折起，使平面
平面
，得到几何体
，如图2所示．
平面
；
和获得等级不是
、
、
，物理、化学、生物获得等级不是
、
、
.
）；
，并说明理由.推荐套卷
（本小题满分12分）已知向量m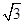＝（sinωx，cosωx），n＝（cosωx,－cosωx）,若函数f（x）＝m·n的图象关于直线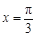对称，其中ω取所有可能值中的最小正数值.
（Ⅰ）求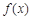的周期和单调递增区间；
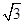（Ⅱ）△ABC中，如果f（）＝，b＝4，且asinA－bsinB＝sinC（c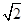－b），求△ABC的面积.
粤公网安备 44130202000953号