设
、
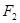分别是椭圆
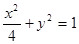的左、右焦点．
（1）若
是该椭圆上的一个动点，求
的取值范围;
（2）设过定点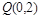
的直线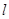
与椭圆交于不同的两点
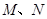，且∠
为锐角（其中
为坐标原点），求直线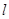的斜率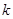
的取值范围．
（3）设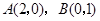
是它的两个顶点，直线
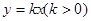与AB相交于点D，与椭圆相交于
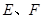两点．求四边形
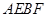面积的最大值
，
，
分别为内角A，B，C的对边且
．
的最大值．(10分)
，
．
，求数列
的前n项和
．
，
，
，且
．
，
，求
的解集．
，
，若
与
的夹角为
，求(1)
（2）求
推荐套卷
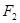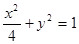设、分别是椭圆的左、右焦点．
（1）若是该椭圆上的一个动点，求的取值范围;
（2）设过定点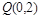的直线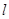与椭圆交于不同的两点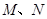，且∠为锐角（其中为坐标原点），求直线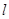的斜率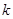的取值范围．
（3）设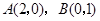是它的两个顶点，直线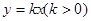与AB相交于点D，与椭圆相交于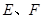两点．求四边形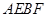面积的最大值
粤公网安备 44130202000953号