已知,如图,△ABC是等边三角形,过AC边上的点D作DG∥BC,交AB于点G,在GD的延长线上取点E,使DE=DC,连接AE、BD.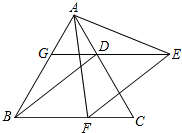
(1)求证:△AGE≌△DAB;
(2)过点E作EF∥DB,交BC于点F,连接AF,求∠AFE的度数.
相关知识点
推荐套卷
已知,如图,△ABC是等边三角形,过AC边上的点D作DG∥BC,交AB于点G,在GD的延长线上取点E,使DE=DC,连接AE、BD.
(1)求证:△AGE≌△DAB;
(2)过点E作EF∥DB,交BC于点F,连接AF,求∠AFE的度数.