(本题满分10分)如图所示,可以自由转动的转盘被3等分,指针落在每个扇形内的机会均等.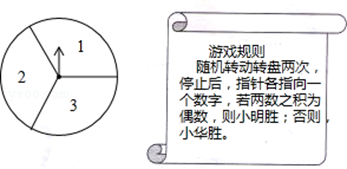
(1)现随机转动转盘一次,停止后,指针指向1的概率为 ;
(2)小明和小华利用这个转盘做游戏,若采用下列游戏规则,你认为对双方公平吗?请用列表或画树状图的方法说明理由.
相关知识点
推荐套卷
(本题满分10分)如图所示,可以自由转动的转盘被3等分,指针落在每个扇形内的机会均等.
(1)现随机转动转盘一次,停止后,指针指向1的概率为 ;
(2)小明和小华利用这个转盘做游戏,若采用下列游戏规则,你认为对双方公平吗?请用列表或画树状图的方法说明理由.