某商店如果将进货价为8元的商品按每件10元售出,那么每天可销售200件.现在采用提高销售价,减少进货量的方法增加利润,已知这种商品每涨价0.5元,其销量就减少10件.
(1)若这种商品涨价2元时,直接写出其销售量;
(2)若设这种商品的销售价为每件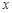 元(
元( ),每天的销售利润为
),每天的销售利润为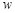 元.
元.
①要使每天获得的销售利润700元,请你帮忙确定销售价;
②问销售价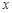 (元)定在多少元时能使每天获得的销售利润最大?并求出此时的最大利润
(元)定在多少元时能使每天获得的销售利润最大?并求出此时的最大利润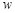 (元).
(元).
相关知识点
推荐套卷
某商店如果将进货价为8元的商品按每件10元售出,那么每天可销售200件.现在采用提高销售价,减少进货量的方法增加利润,已知这种商品每涨价0.5元,其销量就减少10件.
(1)若这种商品涨价2元时,直接写出其销售量;
(2)若设这种商品的销售价为每件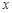 元(
元( ),每天的销售利润为
),每天的销售利润为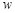 元.
元.
①要使每天获得的销售利润700元,请你帮忙确定销售价;
②问销售价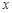 (元)定在多少元时能使每天获得的销售利润最大?并求出此时的最大利润
(元)定在多少元时能使每天获得的销售利润最大?并求出此时的最大利润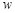 (元).
(元).