如图，已知点B、D、E、C在同一直线上，AB=AC，AD=AE．
求证：BD=CE
（1）根据下面说理步骤填空
证法一：作AM⊥BC，垂足为M．
∵AB=AC（ ） AM⊥BC（ 辅助线 ）
∴BM=CM（ ）
同理DM=EM．
∴BM﹣DM=CM﹣EM（ ）
∴BD=CE（线段和、差的意义）
（2）根据下面证法二的辅助线完成后面的说理步骤．
证法二：作△ABC的中线AM．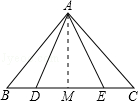
相关试题
如图，已知点B、D、E、C在同一直线上，AB=AC，AD=AE．
求证：BD=CE
（1）根据下面说理步骤填空
证法一：作AM⊥BC，垂足为M．
∵AB=AC（ ） AM⊥BC（ 辅助线 ）
∴BM=CM（ ）
同理DM=EM．
∴BM﹣DM=CM﹣EM（ ）
∴BD=CE（线段和、差的意义）
（2）根据下面证法二的辅助线完成后面的说理步骤．
证法二：作△ABC的中线AM．
的一部分，它经过A
，B
两点．
，D为CB延长线上一点，且BD=2AB．求AD的长
有实数根． 
轴交于点
，
，与
轴交于点
．
的坐标；
交
．在线段
的垂直平分线上是否存在点
，使得点
的距离？如果存在，求出点
作
，将抛物线沿其对称轴平移，使抛物线与线段
总有公共点．试探究：抛物线向上最多可平移多少个单位长度？向下最多可平移多少个单位长度？
粤公网安备 44130202000953号