有三个新兴城镇分别位于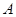
、
、
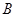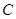三点处，且
，
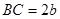，今计划合建一个中心医院，为同时方便三镇，准备建在
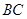的垂直平分线上的
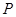点处（建立坐标系如图）．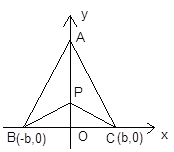
（1）若希望点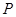到三镇距离的平方和最小，则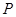应位于何处？
（2）若希望点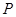到三镇的最远距离为最小，则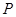应位于何处？
(
≠0)在区间(－1，1)上的单调性。
。
是空集，求
的取值范围；（2）若
，
，
，全集为实数集R。（1）求
，
；（2）若
，求
的取值范围。
，若
，
，求实数
、
的值。相关知识点
推荐套卷
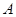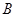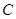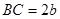有三个新兴城镇分别位于、、三点处，且，，今计划合建一个中心医院，为同时方便三镇，准备建在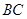的垂直平分线上的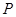点处（建立坐标系如图）．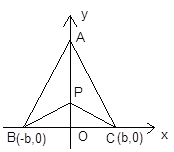
（1）若希望点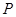到三镇距离的平方和最小，则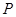应位于何处？
（2）若希望点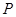到三镇的最远距离为最小，则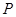应位于何处？
粤公网安备 44130202000953号