（本题7分）某地规定工资收入的个人所得税计算方法如下：
①月收入不超过1200元的部分不纳税；
②收入超过1200元至1700元部分按税率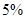
（这部分收入的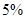，下同）征税；
③收入超过1700元至3000元部分按税率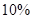
征税。
（1）已知某人某月工资收入是2600元，问他应缴纳个人所得税多少元？
（2）若某人某月缴纳个人所得税65元，问此人本月收入为多少元？（用方程解答，4分）
相关试题
，并从0≤x≤2中选一个你认为合适的整数x代入求值．
，求
的值．
．
．
相关知识点
推荐套卷
（本题7分）某地规定工资收入的个人所得税计算方法如下：
①月收入不超过1200元的部分不纳税；
②收入超过1200元至1700元部分按税率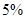（这部分收入的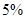，下同）征税；
③收入超过1700元至3000元部分按税率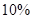征税。
（1）已知某人某月工资收入是2600元，问他应缴纳个人所得税多少元？
（2）若某人某月缴纳个人所得税65元，问此人本月收入为多少元？（用方程解答，4分）
粤公网安备 44130202000953号