如图,直线AB交x轴正半轴于点A(a,0),交y轴正半轴于点B(0,b),且a、b满足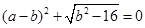 。
。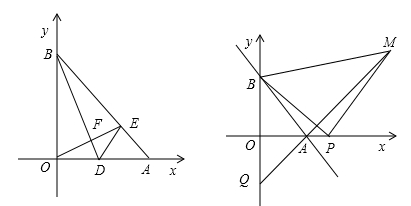
(1)求A、B两点的坐标;
(2)D为OA的中点,连接BD,过点O作OE⊥ BD于 F,交AB于E,求证∠BDO=∠EDA;
(3)如图,P为x轴上A点右侧任意一点,以BP为边作等腰Rt△PBM,其中PB=PM,直线MA交y轴于点Q,当点P在x轴上运动时,线段OQ的长是否发生变化?若不变,求其值;若变化,求线段OQ的取值范围.
相关知识点
推荐套卷
如图,直线AB交x轴正半轴于点A(a,0),交y轴正半轴于点B(0,b),且a、b满足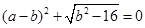 。
。
(1)求A、B两点的坐标;
(2)D为OA的中点,连接BD,过点O作OE⊥ BD于 F,交AB于E,求证∠BDO=∠EDA;
(3)如图,P为x轴上A点右侧任意一点,以BP为边作等腰Rt△PBM,其中PB=PM,直线MA交y轴于点Q,当点P在x轴上运动时,线段OQ的长是否发生变化?若不变,求其值;若变化,求线段OQ的取值范围.