函数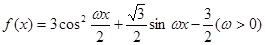
在一个周期内的图象如图所示，
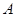为图象的最高点，
、
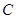为图象与
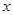轴的交点，且
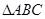为等边三角形。将函数
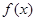的图象上各点的横坐标变为原来的
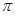倍，将所得图象向右平移
个单位，再向上平移1个单位，得到函数
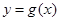的图象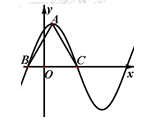
（1）求函数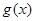
的解析式及函数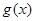的对称中心．
（2）若
对任意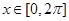
恒成立，求实数
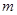的取值范围。
（
，
）为偶函数，其图象上相邻的两个最高点之间的距离为
．
的解析式；（2）若
，
，求
的值．
，求函数在区间
上的单调增区间；
.
，
.
的最小正周期；（2）求
，求
的值.
，
，求
的值.
中，
、
，且
.
、
，猜想
的表达式，并加以证明；
，求证：对任意的自然数
，都有
.相关知识点
推荐套卷
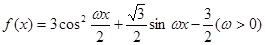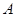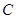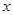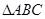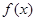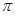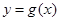函数在一个周期内的图象如图所示，为图象的最高点，、为图象与轴的交点，且为等边三角形。将函数的图象上各点的横坐标变为原来的倍，将所得图象向右平移个单位，再向上平移1个单位，得到函数的图象
（1）求函数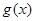的解析式及函数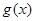的对称中心．
（2）若对任意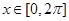恒成立，求实数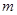的取值范围。
粤公网安备 44130202000953号