某地拟模仿图甲建造一座大型体育馆,其设计方案侧面的外轮廓线如图乙所示:曲线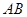 是以点
是以点 为圆心的圆的一部分,其中
为圆心的圆的一部分,其中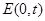 (
( ,单位:米);曲线
,单位:米);曲线 是抛物线
是抛物线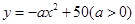 的一部分;
的一部分;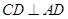 ,且
,且 恰好等于圆
恰好等于圆 的半径. 假定拟建体育馆的高
的半径. 假定拟建体育馆的高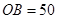 米.
米.
(1)若要求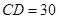 米,
米,
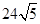 米,求
米,求 与
与 的值;
的值;
(2)若要求体育馆侧面的最大宽度 不超过
不超过 米,求
米,求 的取值范围;
的取值范围;
(3)若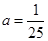 ,求
,求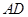 的最大值.
的最大值.
(参考公式:若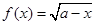 ,则
,则 )
)
推荐套卷
某地拟模仿图甲建造一座大型体育馆,其设计方案侧面的外轮廓线如图乙所示:曲线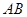 是以点
是以点 为圆心的圆的一部分,其中
为圆心的圆的一部分,其中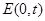 (
( ,单位:米);曲线
,单位:米);曲线 是抛物线
是抛物线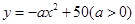 的一部分;
的一部分;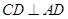 ,且
,且 恰好等于圆
恰好等于圆 的半径. 假定拟建体育馆的高
的半径. 假定拟建体育馆的高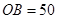 米.
米.
(1)若要求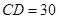 米,
米,
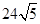 米,求
米,求 与
与 的值;
的值;
(2)若要求体育馆侧面的最大宽度 不超过
不超过 米,求
米,求 的取值范围;
的取值范围;
(3)若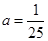 ,求
,求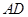 的最大值.
的最大值.
(参考公式:若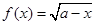 ,则
,则 )
)