(本小题满分12分)
某工厂修建一个长方体无盖蓄水池，其容积为4800立方米，深度为3米．池底每平方米的 造价为150元，池壁每平方米的造价为120元．设池底长方形长为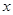
米．
(1)求底面积，并用含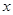的表达式表示池壁面积；
(2)怎样设计水池能使总造价最低?最低造价是多少?
相关试题
中，底面
是正方形，侧棱
底面
是
的中点．
平面
；
与平面
作圆
的弦
，求弦
的轨迹方程．
两点的圆的方程．
和
的交点，且与直线
平行的直线方程；
中，点
，直线
，设圆
的半径为
，圆心在
上。
上，过点
作圆
，使
，求圆心
的取值范围．推荐套卷
(本小题满分12分)
某工厂修建一个长方体无盖蓄水池，其容积为4800立方米，深度为3米．池底每平方米的 造价为150元，池壁每平方米的造价为120元．设池底长方形长为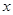米．
(1)求底面积，并用含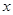的表达式表示池壁面积；
(2)怎样设计水池能使总造价最低?最低造价是多少?
粤公网安备 44130202000953号