先阅读后作答：我们已经知道，根据几何图形的面积关系可以说明完全平方公式，实际上还有一些等式也可以用这种方式加以说明，例如
（2a+b）（a+b） =2a2+3ab+b2,就可以用图的面积关系来说明。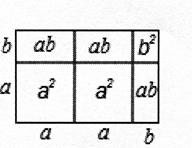
根据下图写出一个等式________________________________________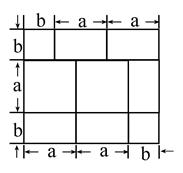
已知等式：（2x+m）（2x+n）=4x2+2（m+n）x+mn．请你画出一个相应的几何图形加以说明。
相关试题
，AB=15，AC=13，求BC的长.如图,直角梯形纸片ABCD中,AD∥BC,∠A=90°,tanC=
.折叠纸片使BC经过点D.点C落在点E处,BF是折痕,且BF=CF=8.
(1)求∠BDF的度数; (2)求AB的长.
如图，一枚运载火箭从地面O处发射，当火箭到达A点时，在观测点C测得其仰角是30°，火箭又上升了10km到达B点时，测得其仰角为60°，求观测点C到发射点O的距离.
(结果精确到0.1km.参考数据：
）.
，AC=18，求：BC、AB的长.
粤公网安备 44130202000953号