如图，在△ABC中，AC＝BC，∠ACB=90°，点D为△ABC内一点，∠CAD=∠CBD=15°，E为AD延长线上的一点，且CE=CA．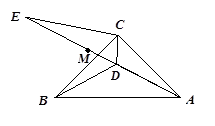
（1）求证：DE平分∠BDC；
（2）若点M在DE上，且DC=DM，请判断ME、BD的数量关系，并给出证明.
相关知识点
推荐套卷
如图，在△ABC中，AC＝BC，∠ACB=90°，点D为△ABC内一点，∠CAD=∠CBD=15°，E为AD延长线上的一点，且CE=CA．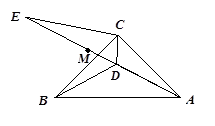
（1）求证：DE平分∠BDC；
（2）若点M在DE上，且DC=DM，请判断ME、BD的数量关系，并给出证明.
粤公网安备 44130202000953号