(本小题满分12分)已知函数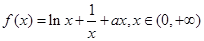 (a是实数),
(a是实数),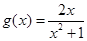 +1。
+1。
(1)若函数f(x)在[1,+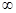 )上是单调函数,求a的取值范围;
)上是单调函数,求a的取值范围;
(2)是否存在正实数a满足:对于任意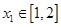 ,总存在
,总存在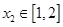 ,使得f(x1)=g(x2)成立,若存在求出a的范围,若不存在,说明理由。
,使得f(x1)=g(x2)成立,若存在求出a的范围,若不存在,说明理由。
(3)若数列 满足
满足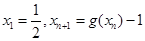 ,求证:
,求证: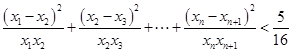 。
。
推荐套卷
(本小题满分12分)已知函数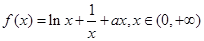 (a是实数),
(a是实数),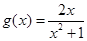 +1。
+1。
(1)若函数f(x)在[1,+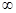 )上是单调函数,求a的取值范围;
)上是单调函数,求a的取值范围;
(2)是否存在正实数a满足:对于任意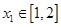 ,总存在
,总存在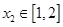 ,使得f(x1)=g(x2)成立,若存在求出a的范围,若不存在,说明理由。
,使得f(x1)=g(x2)成立,若存在求出a的范围,若不存在,说明理由。
(3)若数列 满足
满足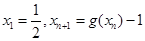 ,求证:
,求证: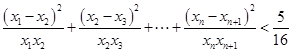 。
。