（本小题满分10分）己知圆
的参数方程为
（
为参数），以坐标原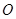点
为极点，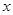
轴的正半轴为极轴建立极坐标系，圆
的极坐标方程为
．
（1）将圆的参数方程化为普通方程，将圆的极坐标方程化为直角坐标方程；
（2）圆，是否相交，若相交，请求出公共弦的长；若不相交，请说明理由．
中，
，
分别为
的三内角
的对边，且
．
；
，且
，求数列
中，
，n≥2时
，求通项公式.
满足
，
（n≥2）.求数列
中，
，前n项的和
，求
.
中，
，且
，（n∈N*），求通项公式
.相关知识点
推荐套卷
（本小题满分10分）己知圆的参数方程为（为参数），以坐标原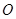点为极点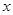，轴的正半轴为极轴建立极坐标系，圆的极坐标方程为．
（1）将圆的参数方程化为普通方程，将圆的极坐标方程化为直角坐标方程；
（2）圆，是否相交，若相交，请求出公共弦的长；若不相交，请说明理由．
粤公网安备 44130202000953号