(本小题满分12分)
如图直线l与x轴、y轴的正半轴分别交于A(8,0)、B(0,6)两点,P为直线l上异于A、B两点之间的一动点. 且PQ∥OA交OB于点Q.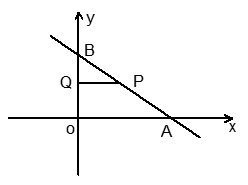
(1)若 和四边形
和四边形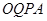 的面积满足
的面积满足 时,请你确定P点在AB上的位置,并求出线段PQ的长;
时,请你确定P点在AB上的位置,并求出线段PQ的长;
(2)在x轴上是否存在点M,使△MPQ为等腰直角三角形,若存在,求出点 与
与 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
推荐套卷
(本小题满分12分)
如图直线l与x轴、y轴的正半轴分别交于A(8,0)、B(0,6)两点,P为直线l上异于A、B两点之间的一动点. 且PQ∥OA交OB于点Q.
(1)若 和四边形
和四边形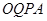 的面积满足
的面积满足 时,请你确定P点在AB上的位置,并求出线段PQ的长;
时,请你确定P点在AB上的位置,并求出线段PQ的长;
(2)在x轴上是否存在点M,使△MPQ为等腰直角三角形,若存在,求出点 与
与 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.