(本小题满分12分)已知抛物线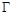 的顶点为坐标原点,焦点为
的顶点为坐标原点,焦点为 .
.
(Ⅰ)求抛物线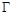 的方程;
的方程;
(Ⅱ)若点 为抛物线
为抛物线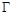 的准线上的任意一点,过点
的准线上的任意一点,过点 作抛物线
作抛物线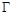 的切线
的切线 与
与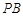 ,切点分别为
,切点分别为 ,求证:直线
,求证:直线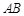 恒过某一定点;
恒过某一定点;
(Ⅲ)分析(Ⅱ)的条件和结论,反思其解题过程,再对命题(Ⅱ)进行变式和推广.请写出一个你发现的真命题,不要求证明(说明:本小题将根据所给出的命题的正确性和一般性酌情给分).
相关知识点
推荐套卷
(本小题满分12分)已知抛物线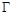 的顶点为坐标原点,焦点为
的顶点为坐标原点,焦点为 .
.
(Ⅰ)求抛物线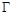 的方程;
的方程;
(Ⅱ)若点 为抛物线
为抛物线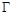 的准线上的任意一点,过点
的准线上的任意一点,过点 作抛物线
作抛物线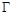 的切线
的切线 与
与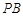 ,切点分别为
,切点分别为 ,求证:直线
,求证:直线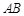 恒过某一定点;
恒过某一定点;
(Ⅲ)分析(Ⅱ)的条件和结论,反思其解题过程,再对命题(Ⅱ)进行变式和推广.请写出一个你发现的真命题,不要求证明(说明:本小题将根据所给出的命题的正确性和一般性酌情给分).