如果一个点能与另外两个点能构成直角三角形,则称这个点为另外两个点的勾股点.例如:矩形ABCD中,点C与A,B两点可构成直角三角形ABC,则称点C为A,B两点的勾股点.同样,点D也是A,B两点的勾股点.
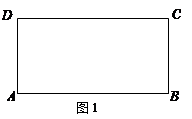
(1)如图1,矩形ABCD中,AB=2,BC=1,请在边CD上作出A,B两点的勾股点(点C和点D除外)(要求:尺规作图,保留作图痕迹,不要求写作法).
(2)矩形ABCD中,AB=3,BC=1,直接写出边CD上A,B两点的勾股点的个数.
(3)如图2,矩形ABCD中,AB=12cm,BC=4cm,DM=8cm,AN=5cm.动点P从D点出发沿着DC方向以1 cm/s的速度向右移动,过点P的直线l平行于BC,当点P运动到点M时停止运动.设运动时间为t(s) ,点H为M,N两点的勾股点,且点H在直线l上.
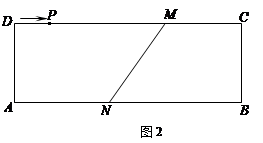
①当t=4时,求PH的长.
②探究满足条件的点H的个数(直接写出点H的个数及相应t的取值范围,不必证明).