在△ABC中，∠A＝90°，AB＝4，AC＝3，M是AB上的动点（不与A，B重合），过M点作MN∥BC交AC于点N．以MN为直径作⊙O，并在⊙O内作内接矩形AMPN．令AM＝x．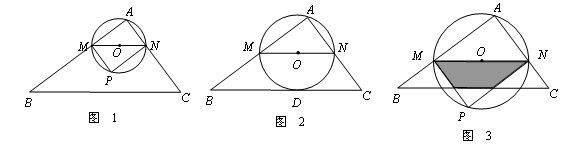 
（1）用含x的代数式表示△ＭNP的面积S；
（2）当x为何值时，⊙O与直线BC相切？
（3）在动点M的运动过程中，记△ＭNP与梯形BCNM重合的面积为y，试求y关于x的函数表达式，并求x为何值时，y的值最大，最大值是多少？
相关试题
．
；
．如图，在平面直角坐标系中完成下列各题：（不写作法，保留作图痕迹）
（1）在图1中作出
关于y轴对称的
，并写出
、
、
的坐标；
（2）在图2中x轴上画出点
，使
的值最小．
；（2）
．
，宽为
（
＞
）的长方形，用剪刀沿图中虚线（对称轴）剪开，把它分成四块形状和大小都一样的小长方形，然后按图（2）那样拼成一个正方形，则中间空的部分的面积是．
相关知识点
推荐套卷
粤公网安备 44130202000953号