如图，抛物线与x轴相交于B，C两点，与y轴相交于点A，点P（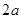
，
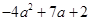）（a是任意实数）在抛物线上，直线
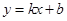经过A，B两点．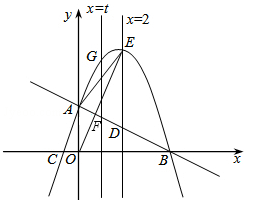
（1）求直线AB的解析式；
（2）平行于y轴的直线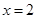
交直线AB于点D，交抛物线于点E．
①直线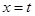
（0≤t≤4）与直线AB相交F，与抛物线相交于点G．若FG∶DE＝3∶4，求t的值；
②将抛物线向上平移m（m＞0）个单位，当EO平分∠AED时，求m的值．
相关试题
，其中
.
（2）
（4）
中，点
是线段
上一动点，
为
的中点，
的延长线交
于
.
；(4分)
，
出发，以1cm/s的速度向
运动(不与
秒，请用
的长；并求
是菱形．(6分)相关知识点
推荐套卷
如图，抛物线与x轴相交于B，C两点，与y轴相交于点A，点P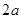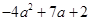（，）（a是任意实数）在抛物线上，直线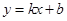经过A，B两点．
（1）求直线AB的解析式；
（2）平行于y轴的直线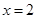交直线AB于点D，交抛物线于点E．
①直线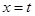（0≤t≤4）与直线AB相交F，与抛物线相交于点G．若FG∶DE＝3∶4，求t的值；
②将抛物线向上平移m（m＞0）个单位，当EO平分∠AED时，求m的值．
粤公网安备 44130202000953号