（本小题满分10分）如图，直线AB与坐标轴分别交于点A、点B，且OA、OB的长分别为方程x2－6x+8=0的两个根（OA＜OB），点C在y轴上，且OA︰AC=1:2，D（3,0）直线CD垂直于直线AB于点P，交x轴于点D。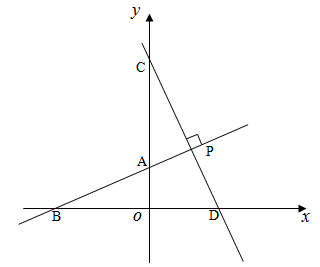
（1）求出点A、点B的坐标。
（2）请求出直线CD的解析式。
（3）若点M为坐标平面内任意一点，在直线AB上是否存在这样的点M，使以点B、D、M为顶点的三角形与△AOB相似，若存在，请直接写出点M的坐标；若不存在，请说明理由。
相关试题
某中学为筹备校庆活动，准备印制一批校庆纪念册。该纪念册每册需要10张8K大小的纸，其中4张为彩页，6张为黑白页。印制该纪念册的总费用由制版费和印刷费两部分组成，制版费与印数无关，价格为：彩页300元/张，黑白页50元/张；印刷费与印数的关系见下表。
| 印数a (单位：千册) |
1≤a＜5 |
5≤a＜10 |
| 彩色 (单位：元/张) |
2．2 |
2．0 |
| 黑白（单位：元/张） |
0．7 |
0．6 |
①印制这批纪念册的制版费为元；
②如果印制2千册，则共需费用元；
③如果该校希望印数至少为4千册，总费用至多为60000元，求印数的取值范围。（精确到0.01千册）
，其中
．（2）
，并写出它的整数解．相关知识点
推荐套卷
粤公网安备 44130202000953号