设数列 满足:①
满足:①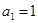 ;②所有项
;②所有项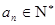 ;③
;③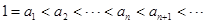 .设集合
.设集合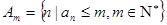 ,将集合
,将集合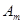 中的元素的最大值记为
中的元素的最大值记为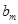 .换句话说,
.换句话说, 是数列
是数列 中满足不等式
中满足不等式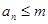 的所有项的项数的最大值.我们称数列
的所有项的项数的最大值.我们称数列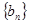 为数列
为数列 的伴随数列.例如,数列1,3,5的伴随数列为1,1,2,2,3.
的伴随数列.例如,数列1,3,5的伴随数列为1,1,2,2,3.
(1)若数列 的伴随数列为1,1,1,2,2,2,3,请写出数列
的伴随数列为1,1,1,2,2,2,3,请写出数列 ;
;
(2)设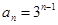 ,求数列
,求数列 的伴随数列
的伴随数列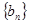 的前100之和;
的前100之和;
(3)若数列 的前
的前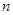 项和
项和 (其中
(其中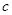 常数),试求数列
常数),试求数列 的伴随数列
的伴随数列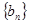 前
前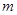 项和
项和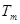 .
.
推荐套卷
设数列 满足:①
满足:①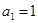 ;②所有项
;②所有项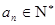 ;③
;③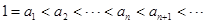 .设集合
.设集合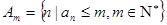 ,将集合
,将集合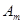 中的元素的最大值记为
中的元素的最大值记为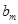 .换句话说,
.换句话说, 是数列
是数列 中满足不等式
中满足不等式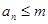 的所有项的项数的最大值.我们称数列
的所有项的项数的最大值.我们称数列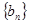 为数列
为数列 的伴随数列.例如,数列1,3,5的伴随数列为1,1,2,2,3.
的伴随数列.例如,数列1,3,5的伴随数列为1,1,2,2,3.
(1)若数列 的伴随数列为1,1,1,2,2,2,3,请写出数列
的伴随数列为1,1,1,2,2,2,3,请写出数列 ;
;
(2)设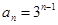 ,求数列
,求数列 的伴随数列
的伴随数列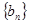 的前100之和;
的前100之和;
(3)若数列 的前
的前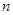 项和
项和 (其中
(其中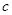 常数),试求数列
常数),试求数列 的伴随数列
的伴随数列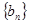 前
前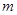 项和
项和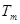 .
.