已知在Rt△ABC,AB=AC,∠BAC=90°,过A的任一条直线AN,BD⊥AN于D,CE⊥AN于E。
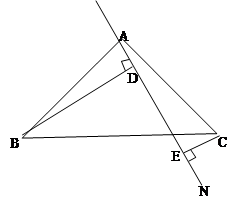
(1)求证:DE=BD-CE
(2)如将直线AN绕A点沿顺时针方向旋转,使它不经过△ABC的内部,再作BD⊥AN于D,CE⊥AN于E,那么DE、DB、CE之间存在等量关系吗?若存在,请证明你的结论?
推荐套卷
已知在Rt△ABC,AB=AC,∠BAC=90°,过A的任一条直线AN,BD⊥AN于D,CE⊥AN于E。

(1)求证:DE=BD-CE
(2)如将直线AN绕A点沿顺时针方向旋转,使它不经过△ABC的内部,再作BD⊥AN于D,CE⊥AN于E,那么DE、DB、CE之间存在等量关系吗?若存在,请证明你的结论?