如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点).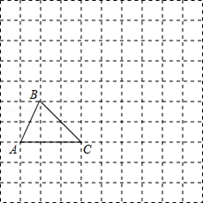
(1)将△ABC绕着点B逆时针旋转90°,得到△A1BC1,请画出△A1BC1;求点A旋转过程中所经过的路径长。
(2)请画一个格点△A2B2C2,使△A2B2C2∽△ABC,且相似比不为1.
相关知识点
推荐套卷
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点).
(1)将△ABC绕着点B逆时针旋转90°,得到△A1BC1,请画出△A1BC1;求点A旋转过程中所经过的路径长。
(2)请画一个格点△A2B2C2,使△A2B2C2∽△ABC,且相似比不为1.