（满分9分）如图，四边形ABCD与四边形CEFH均为正方形，点B、C、E在同一直线上，连接BD，DF，BF。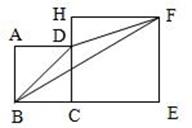
（1）观察图形,直接写出与线段CH平行的线段 ．
（2）图中与线段CH垂直的线段共有_______条。
（3）点B到点F的最短距离为线段____的长，点B到线段EF的的最短距离为线段____的长。
（4）若正方形ABCD的边长为a, 正方形CEFH的边长为2,则线段HD=___,线段BE=___,
此时请你求出三角形DBF的面积，你有什么发现？
（满分9分）如图，四边形ABCD与四边形CEFH均为正方形，点B、C、E在同一直线上，连接BD，DF，BF。
（1）观察图形,直接写出与线段CH平行的线段 ．
（2）图中与线段CH垂直的线段共有_______条。
（3）点B到点F的最短距离为线段____的长，点B到线段EF的的最短距离为线段____的长。
（4）若正方形ABCD的边长为a, 正方形CEFH的边长为2,则线段HD=___,线段BE=___,
此时请你求出三角形DBF的面积，你有什么发现？
，
，
，求a、b、c之间有什么样的关系？
，求n的值.
，
，求
的值.
.
次运算，它工作
秒可作运算多少次？
粤公网安备 44130202000953号