如图，在水平地面点A处有一网球发射器向空中发射网球，网球飞行路线是一条抛物线，在地面上落点为B．有人在直线AB上点C（靠点B一侧）竖直向上摆放无盖的圆柱形桶，试图让网球落入桶内．已知AB＝4米，AC＝3米，网球飞行最大高度OM=5米，圆柱形桶的直径为0.5米，高为0.3米（网球的体积和圆柱形桶的厚度忽略不计）．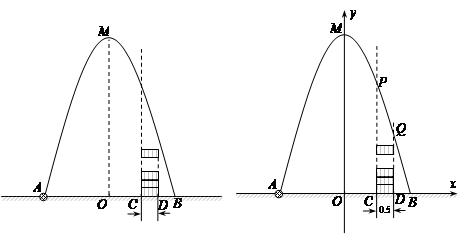
（1）如果竖直摆放5个圆柱形桶时，网球能不能落入桶内？
（2）当竖直摆放圆柱形桶多少个时，网球可以落入桶内？
相关试题
”.小黄误将
，求得结果是
.若
，请你帮助小黄求出一名足球守门员练习折返跑，从球门线出发，向前记作正数，返回记作负数，他的记录如下：（单位：米）＋5，-3，＋10，-8，-6，＋12，-10.
（1）守门员最后是否回到了球门线的位置？
（2）守门员全部练习结束后，他共跑了多少米？
（3）在练习过程中，守门员离开球门线最远距离是多少米？（此小题只写出答案）
， 其中
.
（2） 
（2） 
相关知识点
推荐套卷
粤公网安备 44130202000953号